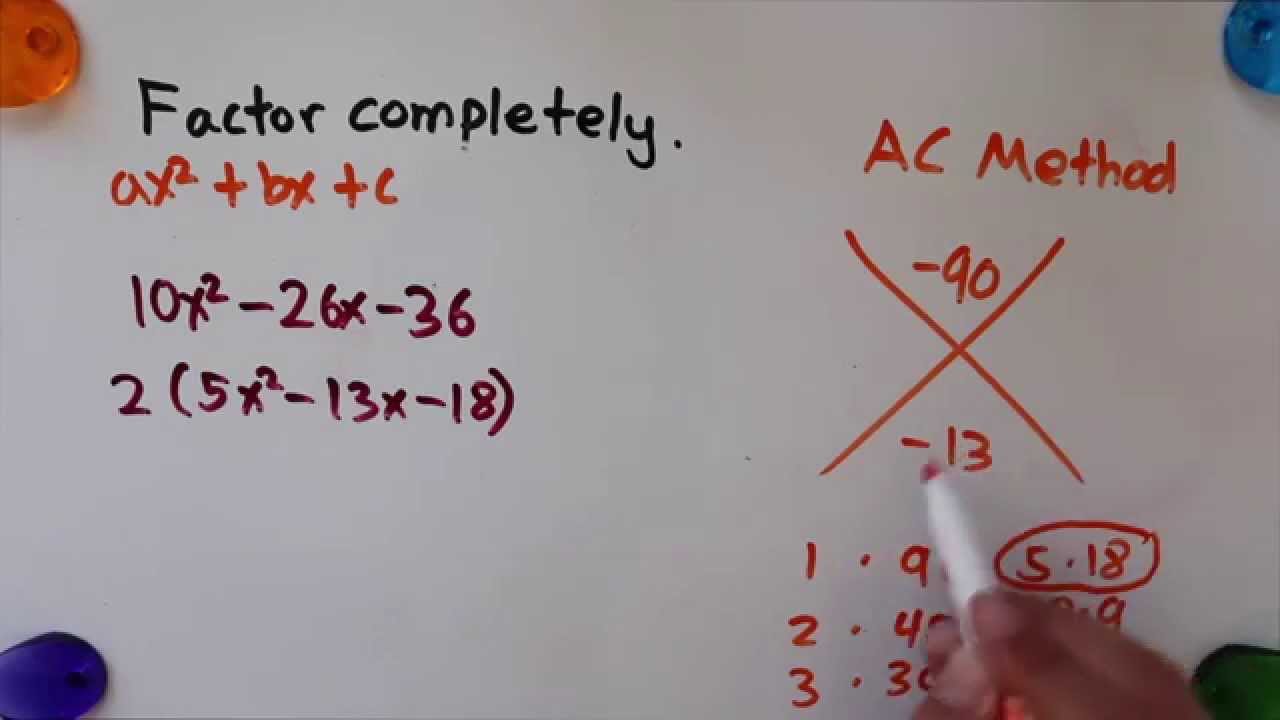Introduction
Factoring quadratic equations is a fundamental skill in algebra that lays the groundwork for solving a wide range of mathematical problems. Quadratic equations take the form ax^2 + bx + c = 0, where a, b, and c are constants, and a is not equal to zero. The process of factoring involves breaking down these equations into simpler expressions, making it easier to find their roots or solutions. In this comprehensive guide, we will delve into the methods, strategies, and techniques for factoring quadratic equations effectively.
I. Factoring Quadratic Equations: The Basics
To understand how to factor quadratic equations, you need to master the fundamental principles involved. Let’s start by examining the basic steps and methods for factoring quadratics.
- Identify the Quadratic Equation: Begin by recognizing the equation as a quadratic. A quadratic equation is in the form ax^2 + bx + c = 0, with ‘a,’ ‘b,’ and ‘c’ as constants.
- Determine the Coefficients: Identify the values of ‘a,’ ‘b,’ and ‘c’ in the equation. These coefficients will guide the factoring process.
- Greatest Common Factor (GCF): One of the most common factoring techniques is to identify the greatest common factor (GCF) among the coefficients. The GCF is the largest number that divides each coefficient evenly. This can be especially helpful when factoring equations with large coefficients.
- Divide by the GCF: Once you’ve identified the GCF, divide each term in the equation by this common factor. This simplifies the equation and sets the stage for further factoring.
- Factor the Expression Inside Parentheses: At this point, you’ll have the GCF factored outside the parentheses. Your goal now is to factor the expression inside the parentheses. This may involve various factoring techniques depending on the equation.
II. Factoring Quadratics with a Leading Coefficient of 1
Quadratic equations where the leading coefficient ‘a’ is equal to 1 are the simplest to factor. These equations follow the form x^2 + bx + c = 0. Factoring them involves finding two numbers that multiply to ‘c’ and add up to ‘b.’ Here’s a step-by-step process for factoring such quadratics:
- Identify ‘b’ and ‘c’: First, determine the values of ‘b’ and ‘c’ in the equation.
- Find Two Numbers: Look for two numbers that multiply to ‘c’ and add up to ‘b.’
- Rewrite as (x + m)(x + n): Rewrite the equation as (x + m)(x + n) = 0, where ‘m’ and ‘n’ are the two numbers found.
- Solve for ‘x’: Set each factor (x + m) and (x + n) equal to zero and solve for ‘x.’ These solutions represent the roots of the quadratic equation.
III. Factoring Quadratics with a Leading Coefficient Other Than 1
Factoring becomes more complex when the leading coefficient ‘a’ is not equal to 1. In these cases, you may need to employ methods like the AC method or trial and error. Here’s a step-by-step process for factoring such quadratics:
- Calculate ‘ac’: Begin by multiplying the leading coefficient ‘a’ by the constant term ‘c,’ which gives you ‘ac.’
- Find Two Numbers: Look for two numbers that multiply to ‘ac’ and add up to ‘b.’
- Rewrite as (dx + m)(ex + n): Rewrite the equation in the form (dx + m)(ex + n) = 0, where ‘d’ and ‘e’ are divisors of ‘a,’ and ‘m’ and ‘n’ are the two numbers found.
- Solve for ‘x’: Set each factor (dx + m) and (ex + n) equal to zero and solve for ‘x.’
IV. Factoring Special Cases
Some quadratic equations follow specific patterns, making factoring quicker and more straightforward. These include:
- Perfect Square Trinomials: Equations in the form (x^2 + 2abx + a^2) = (x + a)^2 and (x^2 – 2abx + a^2) = (x – a)^2 can be factored as perfect squares.
- Difference of Squares: Equations in the form (x^2 – a^2) = (x + a)(x – a) are considered the difference of squares and can be factored easily.
- Quadratics with Repeated Roots: When the discriminant (b^2 – 4ac) is zero, the quadratic equation has repeated roots, which can be factored as (x – p)^2, where ‘p’ is the single root.
V. Tips for Mastering the Art of Factoring Quadratics
- Practice Regularly: Factoring is a skill that improves with practice. Work on a variety of quadratic equations to hone your abilities.
- Understand the Discriminant: The discriminant (b^2 – 4ac) is a key factor in determining the nature of the roots of a quadratic equation. Learn how to interpret its values.
- Pattern Recognition: Be on the lookout for patterns like perfect squares and the difference of squares, which can simplify factoring.
- Check Your Work: After factoring, always verify your work by multiplying the factors to ensure they are equivalent to the original equation.
Conclusion
Factoring quadratic equations is an essential skill in algebra that forms the foundation for solving a multitude of mathematical problems. Whether you’re dealing with quadratics with a leading coefficient of 1 or other values, special cases, or complex solutions, this comprehensive guide has provided you with the knowledge and techniques needed to factor quadratic equations effectively. Factoring is not only a fundamental algebraic skill but also a valuable problem-solving tool. It’s essential for both students and professionals in various fields, from engineering to physics, and even computer science. With practice and a solid understanding of the techniques, you’ll become proficient in this vital aspect of algebra.